Fired clay has been used as an artistic and functional medium for thousands of years. Robert Fathauer brings relatively recent mathematical ideas to this ancient medium, with the goal of creating unique and thought-provoking sculptural forms. In many cases these are reminiscent of forms found in nature, while remaining abstract.

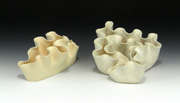
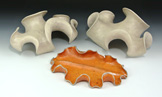
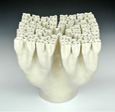
Fractal curves are complex curves that are generated by starting with a single line segment and applying a simple rule repeatedly. Such curves can be used to generate surfaces by spatially separating the different generations of the fractal and then connecting them. Several of Dr. Fathauer's ceramic sculptures are based on fractal curves, though the canonical curves are generally modified by creating curvilinear and/or closed versions.

Spatial development of fractal curves leads to surfaces that grow superlinearly, creating ripples and folding, as is sometimes observed in natural growth structures. These surfaces are related to hyperbolic geometry (in contrast to Euclidean geometry), and they often possess negative curvature. This means the surface curves away from every point in directions of opposite sign, like a saddle.